Recursive Traversal

递归的方法的空间复杂度为O(n)。

节点的定义如下：

// Definition for a binary tree node.
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
}

Preorder Traversal

void preorderTraversal(TreeNode* root, vector<int>& nums) {
    if(!root) return;
    nums.push_back(root->val);
    preorderTraversal(root->left);
    preorderTraversal(root->right);
}

Inorder Traversal

void inorderTraversal(TreeNode* root, vector<int>& nums) {
    if(!root) return;   
    inorderTraversal(root->left, nums);
    nums.push_back(root->val);
    inorderTraversal(root->right, nums);
}

Postorder Traversal

void postorderTraversal(TreeNode* root, vector<int>& nums) {
    if(!root) return;   
    postorderTraversal(root->left, nums);
    postorderTraversal(root->right, nums);
    nums.push_back(root->val);
}

Iterative Traversal

迭代方法需要使用stack来保存遍历路径上待遍历的节点，从根节点到叶节点，最多保存n/2个节点。空间复杂度为O(n)。

Preorder Traversal

// Binary Tree Preorder Traversal
// 使用栈，时间复杂度O(n)，空间复杂度O(n)
class Solution {
public:
    vector<int> preorderTraversal(TreeNode *root) {
        vector<int> result;
        stack<const TreeNode *> s;
        if (root != nullptr) s.push(root);

        while (!s.empty()) {
            const TreeNode *p = s.top();
            s.pop();
            result.push_back(p->val);

            if (p->right != nullptr) s.push(p->right);
            if (p->left != nullptr) s.push(p->left);
        }
        return result;
    }
};

void preorderTraversal(TreeNode* root, vector<int>& nums) {
    vector<int> nums;
    vector<int> nums;
    stack<TreeNode* > st; // pointers in stack are valid

    while (root || !st.empty()) {
        if (!root) {
            root = st.top();
            st.pop();
        }            
        nums.push_back(root->val);
        // if valid right child, push into stack 
        if (root->right) st.push(root->right);

        // go to the left child
        root = root->left;
    }       
    return nums;        
}

Inorder Traversal

// Binary Tree Inorder Traversal
// 使用栈，时间复杂度O(n)，空间复杂度O(n)
class Solution {
public:
    vector<int> inorderTraversal(TreeNode *root) {
        vector<int> result;
        stack<const TreeNode *> s;
        const TreeNode *p = root;

        while (!s.empty() || p != nullptr) {
            if (p != nullptr) {
                s.push(p);
                p = p->left;
            } else {
                p = s.top();
                s.pop();
                result.push_back(p->val);
                p = p->right;
            }
        }
        return result;
    }
};

vector<int> inorderTraversal(TreeNode* root) {
    vector<int> nums;
    stack<TreeNode* > st; // pointers in stack are valid

    while (root || !st.empty()) {
        if (root) {
            // push root into stack, then go left
            st.push(root);
            root = root->left;
        } else { 
            // for nodes in stack, only visit its right
            root = st.top();
            st.pop();
            nums.push_back(root->val);
            root = root->right;
        }
    }
    return nums;
}

Postorder

// Binary Tree Postorder Traversal
// 使用栈，时间复杂度O(n)，空间复杂度O(n)
class Solution {
public:
    vector<int> postorderTraversal(TreeNode *root) {
        vector<int> result;
        stack<const TreeNode *> s;
        /* p，正在访问的结点，q，刚刚访问过的结点*/
        const TreeNode *p = root, *q = nullptr;

        do {
            while (p != nullptr) { /* 往左下走*/
                s.push(p);
                p = p->left;
            }
            q = nullptr;
            while (!s.empty()) {
                p = s.top();
                s.pop();
                /* 右孩子不存在或已被访问，访问之*/
                if (p->right == q) {
                    result.push_back(p->val);
                    q = p; /* 保存刚访问过的结点*/
                } else {
                    /* 当前结点不能访问，需第二次进栈*/
                    s.push(p);
                    /* 先处理右子树*/
                    p = p->right;
                    break;
                }
            }
        } while (!s.empty());

        return result;
    }
};

后序遍历可以看作是和前序遍历是左右对称的，从根节点开始，先遍历右子树，再遍历左子树，只不过为了得到后序遍历的输出，我们需要遍历结果逆序输出。可以比较前序遍历的代码，逻辑完全是一样的，就是左右子树访问顺序交换了，完全是对称的。

vector<int> postorderTraversal(TreeNode* root) {
    vector<int> nums;
    stack<TreeNode* > stnode;

    while (root || !stnode.empty()) {
        if (!root) {
            root = stnode.top();
            stnode.pop();
        }
        nums.push_back(root->val);
        if (root->left) stnode.push(root->left);
        root = root->right;
    }

    return vector<int>(nums.rbegin(), nums.rend()) 
}

• Iterative Postorder Traversal | Set 1 (Using Two Stacks)
• Iterative Postorder Traversal | Set 2 (Using One Stack)

Morris Traversal

Morris遍历方法不需要栈来保存待访问的节点，而是通过利用节点本身的指针来保存待访问节点的指针，并在访问过程中恢复节点。实现了O(1)空间复杂度。

Preorder Traversal

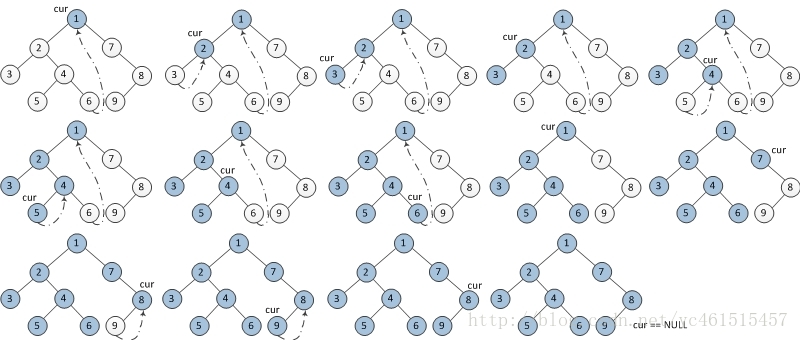
vector<int> preorderTraversal(TreeNode* root) {
    // morris traversal
    vector<int> nums;
    TreeNode* cur = nullptr;

    while (root) {
        if (root->left) {
            cur = root->left;
            // find the predecessor of root node
            while (cur->right && cur->right != root) {                cur = cur->right;
            }

            // has visited this root node
            if (cur->right == root) {
                cur->right = nullptr;
                root = root->right;
            } else {
                nums.push_back(root->val);
                cur->right = root;
                root = root->left;
            }
        } else {
            nums.push_back(root->val);   
            root = root->right;
        }
    }
    return nums;
}

// Binary Tree Preorder Traversal
// Morris先序遍历，时间复杂度O(n)，空间复杂度O(1)
class Solution {
public:
    vector preorderTraversal(TreeNode *root) {
        vector result;
        TreeNode *cur = root, *prev = nullptr;

        while (cur != nullptr) {
            if (cur->left == nullptr) {
                result.push_back(cur->val);
                prev = cur; /* cur刚刚被访问过 */
                cur = cur->right;
            } else {
                /* 查找前驱 */
                TreeNode *node = cur->left;
                while (node->right != nullptr && node->right != cur)
                    node = node->right;

                if (node->right == nullptr) { /* 还没线索化，则建立线索 */
                    result.push_back(cur->val); /* 仅这一行的位置与中序不同 */
                    node->right = cur;
                    prev = cur; /* cur刚刚被访问过 */
                    cur = cur->left;
                } else {    /* 已经线索化，则删除线索  */
                    node->right = nullptr;
                    /* prev = cur; 不能有这句，cur已经被访问 */
                    cur = cur->right;
                }
            }
        }
        return result;
    }
};

Inorder Traversal

中序和前序代码基本一样，唯一不同的在输出节点值的顺序不同。

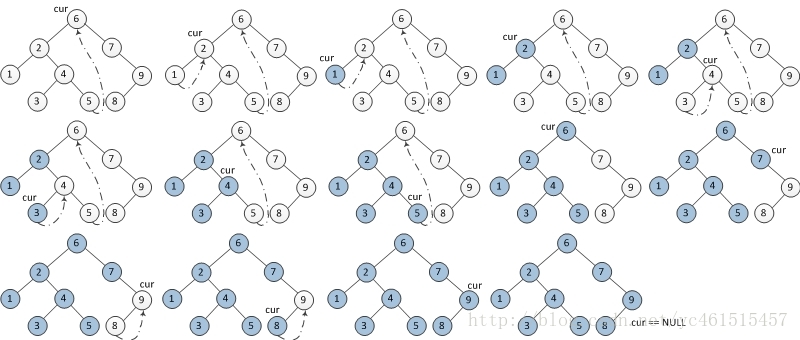
vector<int> inorderTraversal(TreeNode* root) {
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> nums;
        TreeNode* cur = nullptr;

        while (root) {
            if (root->left) {
                cur = root->left;
                while (cur->right && cur->right != root) {
                    cur = cur->right;
                }

                if (cur->right == root) {
                    nums.push_back(root->val);
                    cur->right = nullptr;
                    root = root->right;
                } else {
                    cur->right = root;
                    root = root->left;
                }               
            } else {
                nums.push_back(root->val);
                root = root->right;
            }
        }

        return nums;
    } 
}

// Binary Tree Inorder Traversal
// Morris中序遍历，时间复杂度O(n)，空间复杂度O(1)
class Solution {
public:
    vector inorderTraversal(TreeNode *root) {
        vector result;
        TreeNode *cur = root, *prev = nullptr;

        while (cur != nullptr) {
            if (cur->left == nullptr) {
                result.push_back(cur->val);
                prev = cur;
                cur = cur->right;
            } else {
                /* 查找前驱 */
                TreeNode *node = cur->left;
                while (node->right != nullptr && node->right != cur)
                    node = node->right;

                if (node->right == nullptr) { /* 还没线索化，则建立线索 */
                    node->right = cur;
                    /* prev = cur; 不能有这句，cur还没有被访问 */
                    cur = cur->left;
                } else {    /* 已经线索化，则访问节点，并删除线索  */
                    result.push_back(cur->val);
                    node->right = nullptr;
                    prev = cur;
                    cur = cur->right;
                }
            }
        }
        return result;
    }
};

Postorder Traversal

之前我们在讲迭代方法时，说过了后序遍历其实可以看作是和前序遍历左右对称的，此处，我们同样可以利用这个性质，基于前序遍历的算法，可以很快得到后序遍历的结果。我们只需要将前序遍历中所有的左孩子和右孩子进行交换就可以了。

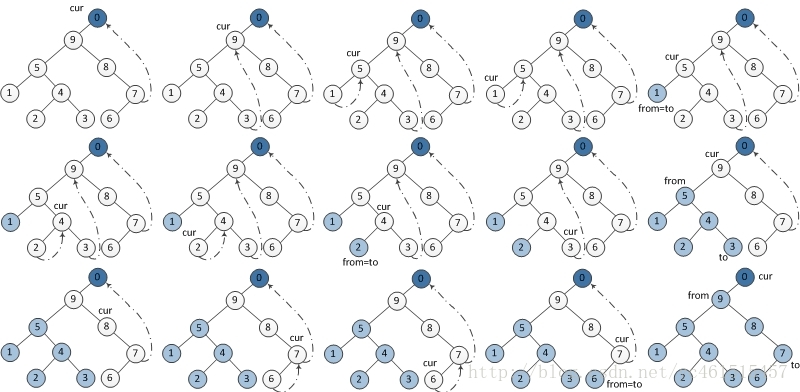
vector<int> postorderTraversal(TreeNode* root) {
    vector<int> nums;
    TreeNode* cur = nullptr;

    while (root) {
        if (root->right) {
            cur = root->right;
            while (cur->left && cur->left != root) {
                cur = cur->left;
            }

            if (cur->left == root) {
                cur->left = nullptr;
                root = root->left;
            } else {
                nums.push_back(root->val);
                cur->left = root;
                root = root->right;
            }

        } else {
            nums.push_back(root->val);
            root = root->left;
        }
    }
    return vector<int>(nums.rbegin(), nums.rend());
}

// Binary Tree Postorder Traversal
// Morris后序遍历，时间复杂度O(n)，空间复杂度O(1)
class Solution {
public:
    vector postorderTraversal(TreeNode *root) {
        vector result;
        TreeNode dummy(-1);
        TreeNode *cur, *prev = nullptr;
        std::function < void(const TreeNode*)> visit = 
            [&result](const TreeNode *node){
            result.push_back(node->val); 
        };

        dummy.left = root;
        cur = &dummy;
        while (cur != nullptr) {
            if (cur->left == nullptr) {
                prev = cur; /* 必须要有 */
                cur = cur->right;
            } else {
                TreeNode *node = cur->left;
                while (node->right != nullptr && node->right != cur)
                    node = node->right;

                if (node->right == nullptr) { /* 还没线索化，则建立线索 */
                    node->right = cur;
                    prev = cur; /* 必须要有 */
                    cur = cur->left;
                } else { /* 已经线索化，则访问节点，并删除线索  */
                    visit_reverse(cur->left, prev, visit);
                    prev->right = nullptr;
                    prev = cur; /* 必须要有 */
                    cur = cur->right;
                }
            }
        }
        return result;
    }
private:
    // 逆转路径
    static void reverse(TreeNode *from, TreeNode *to) {
        TreeNode *x = from, *y = from->right, *z;
        if (from == to) return;

        while (x != to) {
            z = y->right;
            y->right = x;
            x = y;
            y = z;
        }
    }

    // 访问逆转后的路径上的所有结点
    static void visit_reverse(TreeNode* from, TreeNode *to, 
                     std::function< void(const TreeNode*) >& visit) {
        TreeNode *p = to;
        reverse(from, to);

        while (true) {
            visit(p);
            if (p == from)
                break;
            p = p->right;
        }

        reverse(to, from);
    }
};

Ref

• Summary
• Moris
• Video