Linked List Cycle and II

Linked List Cycle

Given a linked list, determine if it has a cycle in it.

Follow up:
Can you solve it without using extra space?

Solution:

为什么有环的情况下二者一定会相遇呢？因为fast先进入环，在slow进入之后，如果把slow看作在前面，fast在后面每次循环都向slow靠近1，所以一定会相遇，而不会出现fast直接跳过slow的情况。

两个指针的速度分别是1和2, 因为两个指针的相对速度是1，所以fast不会越过slow，相遇之前slow指针在环中走过的距离一定小于环的长度。Corner Case: two nodes form a cycle. 相遇时超过cycle和list的长度。

Case 1: whole linked list is a cycle

slow and fast pointers always match at the beginning of the second loop of slow pointer, no matter what total length is odd or even. If fast move 2 nodes and slow move 1 node each step.

Always match in the ending null node.

Slow run 1 loop, whereas fast run 2 loops.

if size n is odd, like 5
slow: 0(head)   1     2        3      4        0
fast: 0(head)   2     4   (4+2)%5=1   3    (3+2)%5=0

n is even, like 6
slow: 0    1    2    3        4    5    0 
fast: 0    2    4 (4+2)%6=0   2    4    0

n is even, like 7
slow: 0    1    2    3     4         5    6     0 
fast: 0    2    4    6  (6+2)%7=1    3    5     0

Case2: part of the linked list is a cycle

以下分析是错误的，因为如果前面链表比较长，slow还没进入链表，但是fast已经在链表内走了m圈了。

there are 2 sub cases: if fast and slow start at the same node, then it falls in to case 1.

0-1-2-3-4 5 6 7 8 9 10 11 -->
    |_______________________|

if fast pointer start 1 nodes ahead of slow pointer

0-1-2-3-4 5 6 7 8 9 10 11 -->
      |_____________________|
      slow start at 3 in the cycle
        fast start at 4 in the cycle.   cycle length is n = 9

if n is odd, n = 5;
slow: 0(head)   1     2        3      4        
fast: 1(head)   3   (3+2)%5=0  2      4
match at the end of first cycle, advanced one node matching point

if n is even, like 6
slow: 0    1    2    3        4    5
fast: 1    3    5 (5+2)%6=1   3    5 
match at the end of first cycle, advanced one node matching point

class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode *fast = head;
        ListNode *slow = head;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
            if (slow == fast) return true;
        }

        return false;
    }
};

Linked List Cycle II

Given a linked list, return the node where the cycle begins. If there is no cycle, returnnull.

Note:Do not modify the linked list.

Follow up:
Can you solve it without using extra space?

fast 的速度是 slow的两倍，即同样的步数，fast走的路程是slow的两倍。设slow距离是s，fast则走了2s。

因为fast先进入环，在slow进入之后，如果把slow看作在前面，fast在后面每次循环都向slow靠近1，所以一定会相遇，而不会出现fast直接跳过slow的情况。相遇之前slow指针在环中走过的距离一定小于环的长度。

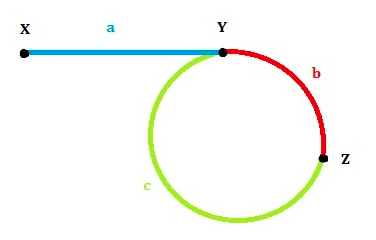r = b + c is the cycle length, Z is the first time matching point

We have S_s = a + b, since S_f = 2 * S_s, that is S_f = 2 (a + b) 
we also have S_f = a + b + n*r = a + b + n*(b+c),  (fast have run n cycles before the first matching)
then we have 2(a+b) = a + b + n*r,  that is a+b=n*r= (n-1)r + r
Set the total length of the Linked List is L, we have r = L-a
So a + b = (n-1)r + L-a, then a = (n-1)r + L-a-b = (n-1)r + c

Then we know, when we first match, we can have a second slow pointer whose speed is 1 the same as the first slow pointer. First slow pointer begin at Z, second slow pointer begin at X, they will match at Y.

We can also think in this way, the fast pointer run (n-1) cycles , and then firstly match the first slow pointer at Z, there are c or a left distance need to be done.

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *fast = head, *slow = head;
        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
            if (fast == slow) {
                ListNode* slow2 = head;

                while (slow2 != slow) {
                    slow = slow->next;
                    slow2 = slow2->next;
                }
                return slow2;
            }
        }
        return nullptr;
    }
};

Linked List Cycle and 2

Linked List Cycle and II